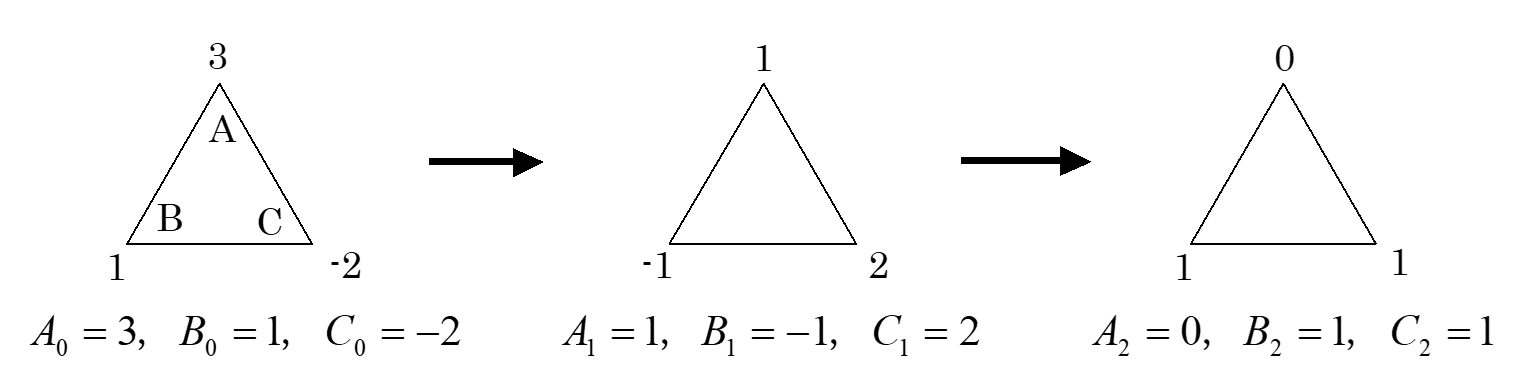第003回問題

無限にある整数について証明するときに使う方法に「数学的帰納法」があります。一方、なにかが有限であることを証明するときに使う方法に「無限降下法」というものがあります。背理法と合わせてよく使われる証明方法の1つです。
17世紀の数学者フェルマーはこの方法を得意としていました。フェルマーは数学の本を読むとき、その本に関する発見や感想を余白に書く癖があったと言われていますが、その書き込みの1つに
「2つの立方数の和に分けることはできない。4乗数を2つの4乗数の和に分けることはできない。一般に、冪が2より大きいとき、その冪乗数を2つの冪乗数の和に分けることはできない。この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。」という書き込みがあります。この命題は、その後数百年に渡って数学者を悩まし続け、「フェルマーの最終予想」と呼ばれていましたが、20世紀後半に数学者アンドリュー・ワイルズによって証明されました。おそらく、フェルマーはこの命題を無限降下法で解けると誤解したのではないかと言われています。

正三角形ABCの頂点に実数がふられており，少なくともそのうちの１つは負で，3つの数の和は正である。今，ある頂点にふられた数が負のとき，次のような操作を行う。 操作)　他の2つの頂点にその数を足す。次にその頂点の符号を入れ替えて正の数にする。 この操作は1回につき1つの頂点について行い，頂点にふられた数に負の数がある限り行いつづけるものとする。また，$n$回目の操作によって得られた頂点A，B，Cにふられた数をそれぞれ $A_n,B_n,C_n$とする。（操作を行う前を$n=0$ とする。） 例えば，三頂点に3，1，-2がふられていた場合は次のようになって，操作は2回で終了する。次の問いに答えよ。 (1)　 $S_n = A_n+B_n+C_n$とするとき， $S_n$と $S_n+1$との大小を比較せよ。 (2)　 $A_0+B_0+C_0>0$ で$A_0,B_0,C_0$のうち1つは負の数であるとする。初期値として、$A_0 , B_0 , C_0$ をどのように設定しても、この操作は有限の回数で必ず終了することを証明せよ。

印刷用PDFはこちらからダウウンロードできます。

解答はこちら（5/23以降に公開）
前の回の問題

数学好きのためのちょっと考える演習問題一覧に戻る

あなたの解答をお待ちしています。別解やもっと面白い解き方があったとき、あるいは数学の本で見つけた関連する知識などあればぜひメールをください。（メールの宛先：web_info–marugame-ict.org　–を@に変えてください。）